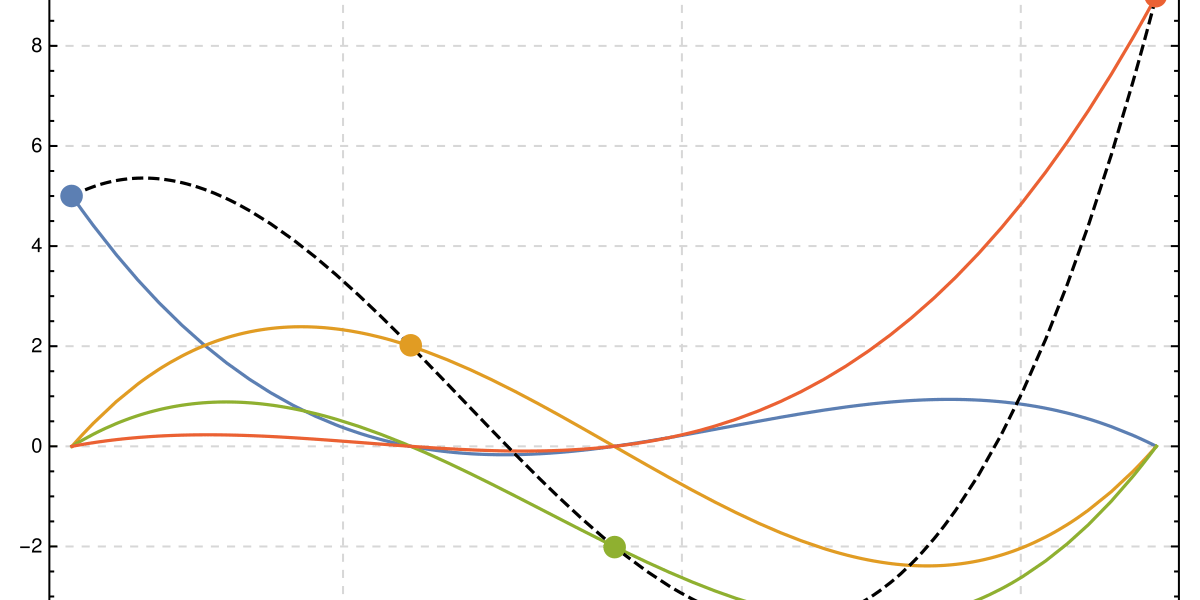
Here is the Lagrange interpolating polynomial equation:
![\[ L_i(X)=\prod_{j=0\atop j \ne i}^n\frac{(X-a_j)}{(a_i-a_j)} \]](https://cdn.trevalim.fr/wp-content/ql-cache/quicklatex.com-54388f78f529c6f6a7127253eeeb1b56_l3.png "Rendered by QuickLaTeX.com")
![\[ \boxed{P=\sum_{i=0}^nP(a_i)L_i(X)} \]](https://cdn.trevalim.fr/wp-content/ql-cache/quicklatex.com-27e8eb326ac64113981495013f168431_l3.png "Rendered by QuickLaTeX.com")
You can find a python code hosted in GitHub here: https://github.com/eddydu44/Lagrange-interpolating-polynomials
It calculates the polynomial that passes through points given interactively.
And it plots a graph like these ones :
Code :
| from functools import reduce | |
| from sympy import Symbol | |
| X = Symbol('X') | |
| def Lagrange(points): | |
| P=[reduce((lambda x,y: x*y),[(X-points[j][0])/(points[i][0] - points[j][0]) for j in range(len(points)) if i != j])*points[i][1] for i in range(len(points))] | |
| return sum(P) | |
| print("Enter every points in this format : x y \nStop the list by entering 0") | |
| p1=0 | |
| points=[] | |
| while True: | |
| p1 = [int(x) for x in input("Enter point coord: ").split()] | |
| if p1 == [0]: | |
| break | |
| points+=[p1] | |
| print(points) | |
| P=Lagrange(points) | |
| print("\nLagrange equation :\n") | |
| print(P) | |
| import matplotlib.pyplot as plt | |
| from numpy import arange | |
| def graph(P,points): | |
| plt.plot([points[i][0] for i in range(len(points))], [points[i][1] for i in range(len(points))], 'ro') | |
| plt.title('P(X)=' + str(P)) | |
| xmin=min([points[i][0] for i in range(len(points))])-1 | |
| xmax=max([points[i][0] for i in range(len(points))])+1 | |
| t1 = arange(xmin, xmax, 0.02) | |
| def f(t): | |
| t2 = [] | |
| for i in t : | |
| t2 += [P.subs(X,i)] | |
| return t2 | |
| plt.plot(t1,f(t1),'r--') | |
| plt.show() | |
| graph(P,points) |
Ni vu ni connu ! D’une simple commande vous pourrez cacher tout ce que vous voudrez ! 1) Créer une archive avec […]
Redirect every mobiles to the amp version of the site with map and try files.
